von Christina Unger

Die Ideologie trennt Menschen, die Logik bringt sie zusammen - Ein kurzer Ausschnitt polnischer Logik

Als Polen 1918 seine Unabhängigkeit zurückgewann, war in Warschau gerade erst die Universität wiedereröffnet worden und die polnischen Gelehrten begannen damit, ein nationales akademisches Leben aufzubauen. In den darauffolgenden zwei Jahrzehnten entwickelte sich Polen zu einem der Logikzentren der Welt.

Als Vater der polnischen Logik gilt Kazimierz Twardowski, der bei Franz Brentano in Wien Philosophie studiert hatte und 1895 auf den Lehrstuhl für Philosophie der Universität in Lwow berufen wurde. Er verfolgte ehrgeizig den Plan, eine organisierte, wissenschaftliche Philosophie in Polen aufzubauen – ein Ziel, dem er sogar seine eigene Forschung unterordnete. Anfangs lehrte Twardowski vor fast leeren Hörsälen. Aber dank seiner außergewöhnlichen Lehrbegabung und seiner charismatischen Persönlichkeit zog er immer mehr Studierende zur Philosophie, bis schließlich etwa 200 Studierende an seinen Seminaren und ungefähr 2000 an seinen Vorlesungen teilnehmen wollten und er aus Platzmangel außerhalb der Universität lehren musste.

Kazimierz Twardowski

Zu seinen Schülern zählten neben Lukasiewicz auch Ajdukiewicz (einer der Logiker, auf die die Kategorialgrammatik zurückgeht) und Kotarbinski (der u.a. zur Erkentnnistheorie arbeitete). Ab 1910 war auch Lesniewski (der ein formales Ontologiesystem als Alternative zur Mengentheorie entwickelte) in Lwow und als er und Lukasiewicz wenige Jahre später eine Professur in Warschau annahmen, war die Achse Lwow-Warschau aufgemacht und die Lwow-Warschau-Schule zum Leben erweckt. Diese zeichnete sich v.a. durch die enge Verbindung von Philosophie und Mathematik aus. Twardowski forderte einen Philosophiestil, der Ideen klar und eindeutig formuliert, präzise analysiert und die Ergebnisse durch eine klare Argumentation rechtfertigt. Für die Umsetzung dessen wurde in der Lwow-Warschau-Schule die Logik das grundlegende Werkzeug. Twardowski war zwar selbst kein Logiker, er schuf aber eine Atmosphäre, die aufgeschlossen und fördernd war für alle, die Logik als die wichtigste Quelle methodologischer Kriterien ansahen und philosophische Probleme mit den Methoden der Logik und Mathematik untersuchen und lösen wollten. In Polen wurde die mathematische Logik längst als eigenständiger Forschungszweig angesehen und einer derjenigen, der sich ihr voll und ganz widmete, war Jan Lukasiewicz.

Lukasiewicz war Twardowskis erster Schüler in Lwow. Er schrieb 1902 seine Doktorarbeit, war dann einige Zeit in Berlin und Louvain, kehrte 1906 als Dozent nach Lwow zurück und wurde schließlich Professor für Logik und Philosophie in Warschau, wo er die ersten polnischen Kurse über mathematische Logik hielt. Zwei sehr bekannte Errungenschaften von ihm sind die Polnische Notation und mehrwertige Logiken.

Die Polnische Notation ist eine sehr ökonomische, klammerfreie Notation logischer Formeln, in der logische Konstanten vor ihre Argumente geschrieben werden. Statt , , , und für die logischen Operationen verwendete Lukasiewicz die Buchstaben N (für Negation), K (für Konjunktion), A (für Disjunktion), C (für Implikation) und E (für Äquivalenz). Jede Formel der Aussagenlogik beginnt mit einem solchen Großbuchstaben, der das Hauptverknüpfungszeichen der Formel ist und von Variablen gefolgt wird oder von Formeln, die ihrerseits auch wieder aus Konstanten und Variablen bestehen. Z.B. enthält Lukasiewiczs Axiomensystem für die Aussagenlogik (zusammen mit der Substitutionsregel und dem Modus Ponens) drei Axiome, die in polnischer Notation folgendermaßen aussehen: CCpqCCqrCpr, CCNppp, CpCNpq. Einmal soll es vorgekommen sein, dass Lukasiewicz über eine Fomeln, die mit CCCKCCKCKKKKCCCKC... anfing, freudig sagte: "Wie schön und offensichtlich wahr es doch ist!"

Mit der Entwicklung mehrwertiger Logiken geht auf Lukasiewicz außerdem das erste nicht-klassische Logikkalkül zurück. Ausgangspunkt dafür war, dass kein möglicher Funktor der klassischen Logik als "es ist möglich, dass" interpretiert werden kann. Die Formel Mp (für "es ist möglich, dass p") soll trotzdem extensional sein, ihr Wahrheitswert also nur vom Wert von p abhängen. Lukasiewiczs Lösung bestand darin, einen dritten Wahrheitswert zuzulassen. So ist z.B. der Satz "Robert Förster wird die Tour de France gewinnen" weder wahr noch falsch, sondern möglich, und bekommt genauso wie seine Negation den Wahrheitswert 1/2 zugewiesen. Lukasiewicz verallgemeinerte diese dreiwertige Logik zu mehrwertigen Logiken mit bis zu abzählbar unendlichen vielen Werten zwischen 0 und 1. Die Wahrheitswertfunktionen sind dann allgemein angegeben, die Negation z.B. durch Np=1-p (wobei 0 =< p =< 1). Lässt man nur die zwei Werte 0 und 1 zu, ergibt sich daraus die klassische Negation. Die Ansicht, dass eine dieser Logiken eine korrekte Beschreibung der tatsächlichen Welt liefert, gab Lukasiewicz im Laufe der Zeit auf, trotzdem glaubte er, dass mehrwertige Logiken eine wichtige Rolle für die Grundlagen der Mathematik spielen würden.

Zu den Schülern von Lukasiewicz in Warschau gehörte Alfred Tarski, der heute zusammen mit Aristoteles, Frege und Gödel zu den größten Logikern gezählt wird. Eines seiner Ziele war, eine präzise Definition für den Begriff der Wahrheit und der logischen Folgerung zu geben. Eines seiner Kriterien an eine Definition von Wahrheit in einer formalen Sprache war, dass die Sätze, die das Wahrheitsprädikat erfüllen, genau die sind, die wir intuitiv als die wahren Sätze der Sprache ansehen. Diese Intuition kann dadurch erfasst werden, dass für jeden Satz das T-Schema „True('S') genau dann, wenn S“ beweisbar sein soll, wobei 'S' der Satz in der Objektsprache und S seine Entsprechung in der Metasprache ist. Tarski zeigte, dass das Wahrheitsprädikat nicht in der Objektsprache, sondern in der Metasprache definiert sein muss. Denn sobald die Objektsprache über ihre eigene Semantik reden kann, lassen sich Sätze wie "Dieser Satz ist nicht wahr" formulieren. Ausgehend von einem Begriff der Erfüllbarkeit definierte Tarski Wahrheit dann wie folgt:

Ein Satz S ist wahr genau dann, wenn S von jeder Variablenbelegung erfüllt wird.

Seine Wahrheitsdefinition für formale Sprachen war der erste Schritt hin zur Modelltheorie und ist heute genauso Standard wie auch seine Definition der logischen Folgerung:

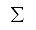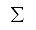Ein Satz S folgt logisch aus einer Menge Sigma von Sätzen genau dann, wenn jedes Modell von Sigma auch ein Modell von S ist.

Tarski arbeitete u.a. auch zu Entscheidungproblemen, zur Mengenlehre, zur Axiomatisierung von Algebra und Geometrie, und zusammen mit dem polnischen Mathematiker und Logiker Adolf Lindenbaum zur Algebraisierung der Logik.

Alfred Tarski

Der hereinbrechende zweite Weltkrieg hatte katastrophale Auswirkungen für die polnische Logik. Strukturen zwischen wissenschaftlichen Institutionen wurden zerstört und die Judenverfolgung kostete mehreren Logikern, Philosophen und Mathematikern das Leben. Tarski, der sich weit mehr als Pole denn als Jude fühlte und schon vor Jahren zum Katholizismus konvertiert war, war sich dem Ernst der Lage nicht bewusst und entkam nur sehr knapp dem Schicksal, dem viele seiner jüdischen Kollegen zum Opfer fielen. Er hatte eine Einladung zur "Unity of Science"-Tagung in den USA und in der festen Überzeugung, nur zwei Wochen weg zu sein, ließ er Frau und Kinder in Warschau zurück und verließ Polen mit dem letzten Schiff, bevor es keinen legalen Weg mehr gab, das Land zu verlassen. Die Logikerin Janina Hosiasson-Lindenbaum wollte an derselben Konferenz teilnehmen und mit dem nächsten Schiff nach Nordamerika aufbrechen, aber ihr wurde das Visum verwehrt. Sie und ihr Mann Adolf Lindenbaum wurden 1941 im Ghetto in Vilnius ermordet.

Lukasiewicz wanderte 1946 wegen Unzufriedenheit mit dem politischen System nach Dublin aus, während Tarski in Berkeley ein Forschunsgzentrum ausbaute. Sie und andere Anhänger der Lwow-Warschau-Schule führten deren Ideen zwar außerhalb von Polen weiter, als organsierte Schule war sie aber vollständig auseinandergebrochen.